Solving & Generating Nurikabe Puzzles

Nurikabe was invented by the company best known for popularizing Sudoku, but is, at least in my view, a much better puzzle. At the very least, it is probably a much harder one.

The rules are simple:

• We are given a board and are asked to color the tiles as land and sea.
• We are given one tile from each island, and its size.
• We must keep the entire sea (orthogonally) connected.
• We can’t have any “pools”, or 2x2 squares of sea.

For example, given this starting board below, we can make some easy progress:

This is an easy puzzle, and there’s plenty more easy progress to be made. In fact, these three rules are almost enough to solve it entirely. My most recent project, a Nurikabe solver, solved it in 9.9 milliseconds (after generating it in 180). However, these puzzles can get very difficult, for example, in the following position it is not at all obvious how to proceed:

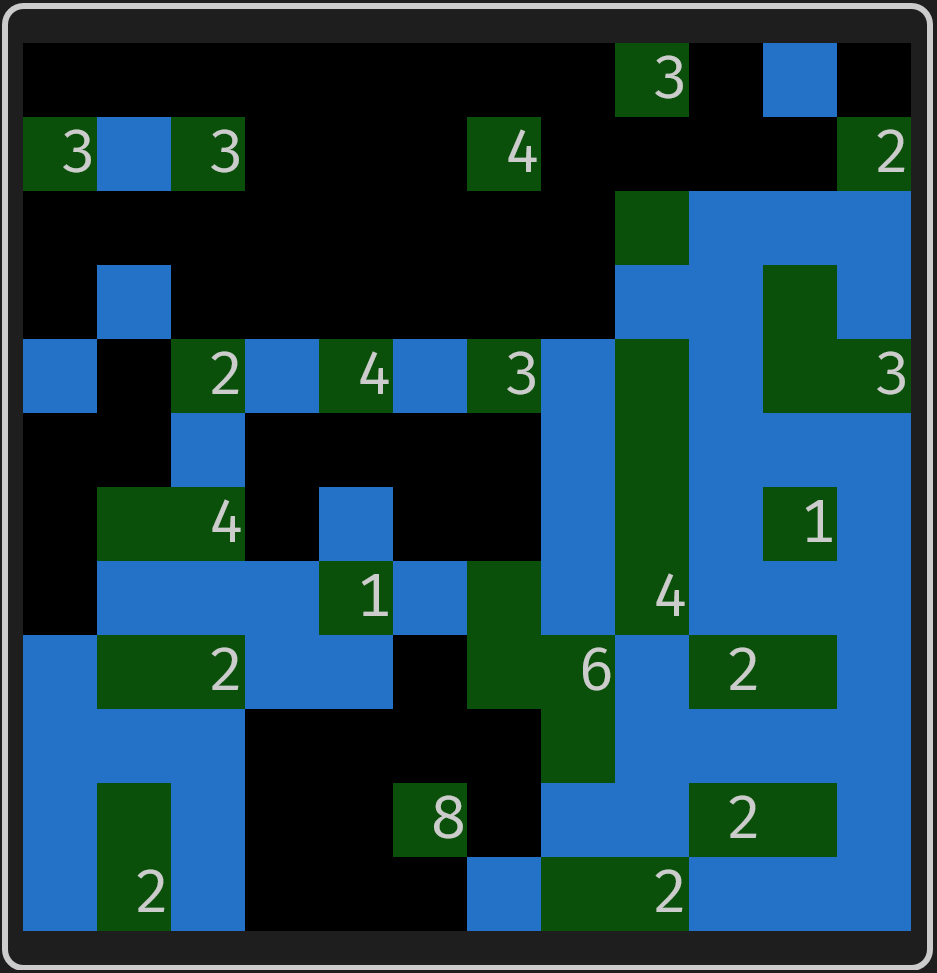
The goal of this project was to create a Nurikabe solver which can give step-by-step advice, especially in tough positions like this one. I didn’t just want to solve the puzzles, I also wanted to understand the solutions, and I wanted to have as little guessing as possible.

Solver Rules

The solver has a list of rules it tries to apply, in roughly increasing order of complexity. Whenever we make any progress, we return to the start of the list, and try the simpler rules again.

Here, “progress” does not necessarily mean we’ve colored in any new tiles. Instead, we keep a running list of possibilities for each tile. Initially, any tile could be part of any island, or part of the sea. As we apply our rules, we whittle down the space of possiblities until there is only one possibility remaining for each tile: “progress” just means that we’ve eliminated at least one possibility for at least one tile.

The full list of rules can be found here, but the main ones are these:

1. If we detect a ‘contradiction’, we immediately start backtracking. These contradictions can look like:
   • A 2x2 pool.
   • A sea tile which is unreachable from a sea tile (so that the sea can never be made contiguous).
   • An island without enough space to reach its size.
2. If an island is complete, we surround it with water.
3. If we detect an L-corner, we fill in the corner space with land.
4. If an incomplete island (or sea) can only be extended in one direction, we do so.

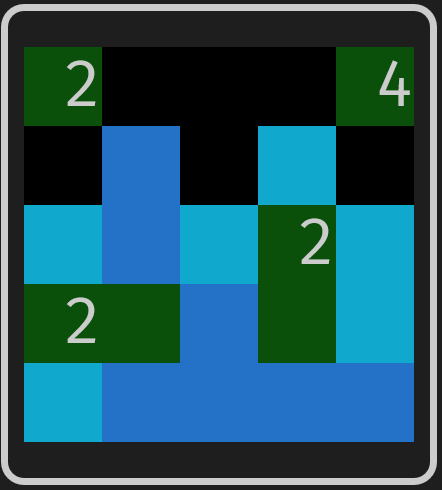
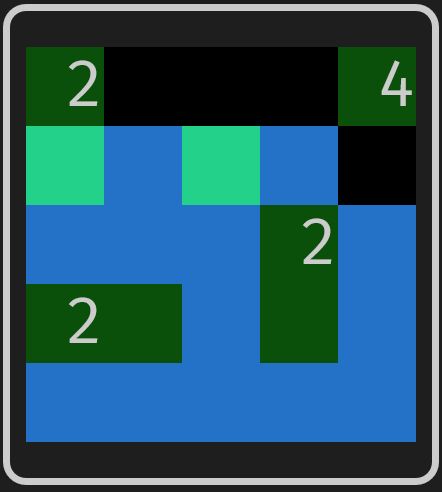
5. If a tile is not reachable by any islands, then it must be sea.
6. If a tile borders more than one island, then it must be sea.
7. If making a tile land would create a path between two edges of the board (creating a disconnected sea) then it must be sea.
8. If a tile is surrounded by land, then it must be land.
9. If an island has too little space to avoid a tile, than that tile must be part of that island.

10. If all the possible paths an island border a tile, then that tile must be sea.
11. The last rule is that if two empty cells border two adjacent walls, and the only way to reach one empty cell is to pass through the other, then the nearer cell is land (Since otherwise, we would have a 2x2 pool).

Guessing

These rules are enough to solve many puzzles, even of intermediate difficulty, but Nurikabe is NP-hard, so we (probably) can’t hope to get by without any guessing at all (or at least, without something computationally equivalent).

After we make a guess (whatever form that takes), we will eventually reach one of 2 possibilities:

1. We reach an invalid board state. In this case, we know our original guess was wrong, and can be removed from our set of possibilities.
2. We reach a solved board state. In this case, we can’t simply deduce that our guess was correct, since there may be other solutions in which our guess doesn’t hold. Instead, we just take note of the fact that a solution has been found, and see if there are any others. If not, then our first solution is the correct one. Well-designed puzzles should have unique solutions, but we should be able to detect when this is not the case.

We can use iterative deepening search to try to find the solution that requires the least amount of nested guessing. Again, our goal is not just to solve the board, but to find the simplest solution we can.

Board Generation

This is a classic hay-in-haystack problem: The good news is that Nurikabe puzzles are very common. The bad news is that we have to pick one. We are trying to choose clues that specify a board uniquely, but the difficulty here is that since there are so many possible Nurikabe boards, we’ll have to make a lot of arbitrary choices before we are left with only one solution.

Basically, board generation is a guess-and-check game. This can be done many ways (several of which I took a good stab at), but by final algorithm works in 3 phases:

Phase 1: Tiling Generation

In the first stage, we ignore the numbers entirely, and just focus on creating a valid green/blue assignment of tiles on the board. In my algorithm, this is done by starting with an empty board, then placing islands one-by-one. Between each placement, we’ll consult our solver to see if our placements have any implications for our tiling, so that we can avoid creating contradictions before they arise.

Phase 2: Labelling

Next, we try labelling the islands of our tiling many different ways, trying to find one which provides the most information about the board. Doing this randomly yields poor results, so I used a Metropolis-Hastings approach: start with a random approach, then repeatedly tweak it. At each step, we assign the clues a score based on how much of the board they reveal, and use this to determine whether to use the new board or to keep the old one.¹

Phase 3: Amendments

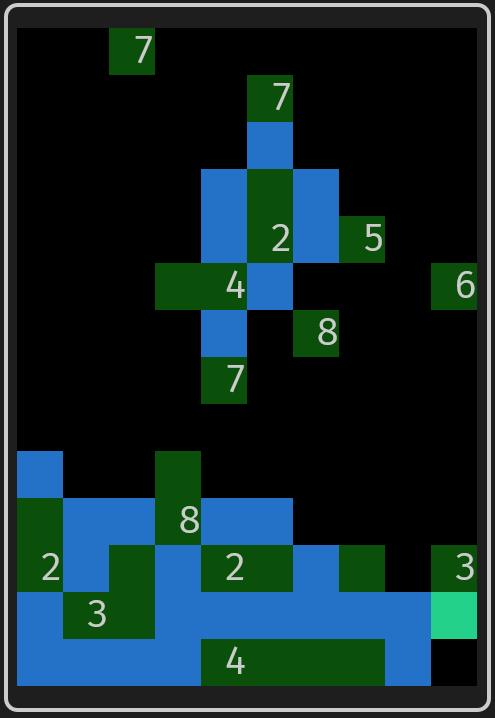
Usually, phase 1 & 2 are enough to tile the board almost (but not quite) completely. For example:

This board almost works, but there are minor issues. However, we could increment the unfinished labels to finish things off. This is often the case, so when a board is nearly complete, I give it a few chances to redeem itself by incrementing the labels of unfinished tiles. It would probably be helpful to do something more sophisticated (maybe reaching for the Metropolis-Hastings hammer again…), but this will do.

Each of the above steps may fail, so we need to limit how many times we try each one. (This can be done without too much regret, there’s lots of hay out there…)

Results

We have a lot of dials to turn to customize our process: the size of our board, the average island size, how many times we try relabelling our board, what solving rules we use throughout the generation, etc…

On the whole, things get tough if we try to generate boards much larger than a 12x12. I benchmarked the results of generating a 14x10 grid with small islands (max size 5, mean size 2), and got a mean generation time of 12s and a standard deviation of 10s. Could definitely be worse.

Other Solvers

Having spent a meaningful amount on this problem, I’m absolutely baffled how this site generated 11 million 20x20 boards (even if they have small islands).²

I was also really impressed by this solver/generator, which is much faster than mine, though I found that it uses simpler rules than mine, so it generates easier puzzles and is unable to solve some harder ones. For example, it gets stuck on the puzzle below, generated by my generator (solution here):

However, from a human perspective, its puzzles can hardly be called easy, and its algorithm looks like a simpler, faster version of mine: phase 1 is similar but randomly places the sea instead of the islands, phase 2 is done deterministically, instead of randomly, and phase 3 just adds and removes walls randomly.

Maybe all of this is a lesson about Occam’s razor and avoiding overengineering, or maybe it’s a sign to switch to Javascript. Who knows…